Scientific evidence vs statistical evidence

Formal scientific evidence is impossible, yet statistics makes formal claims all the time. What gives?

I. Confirmationism and Hempel's paradox

A false but intuitive view of science is that we run around and collect evidence in favor of various theories. The theory that has the most evidence in its favor wins and is our go to theory until the evidence starts to favor another hypothesis. This is the confirmationist view of science: We look for evidence that supports our theories, and those with more evidence in their favor are more likely to be true.

The confirmationist view sounds good until you start to formalize the notion of evidence. There are several issues, but a particularly devastating one is Hempel's paradox.

Suppose we have the theory: All monkeys have prehensile tails. (A prehensile tail is a tail that can hold objects.) The logician would write this as the conditional statement: If x is a monkey, then x has a prehensile tail. The contrapositive of this statement is: If x does not have a prehensile tail then x is not a monkey. The contrapositive of a statement is logically equivalent to the original statement, so evidence for one is evidence for the other. (Release your inner Wittgenstein and draw a simple truth table if you're unconvinced, or read wikipedia's intuitive explanation.)

Hempel's paradox is the observation that we can get endless evidence for the statement If x does not have a prehensile tail then x is not a monkey by simply noticing that things that don't have tails are, in fact, not monkeys. No tail on my air conditioner? Check. No tail on my laptop? Sweet, sweet evidence. No tail in my coffee? I think we have a pretty damn good theory on our hands!

Karl Hempel. Word on the street is that his original example was “All Hempels have square heads.” Either that or it was about ravens.

This is extremely unsatisfying. We can get arbitrary confirmation of our theory concerning monkeys and tails by examining non-monkeys with no tails. The race to confirm the theory thus becomes a race to observe the most non-monkeys.

So where do we go from here? Except for a few rogue philosophers who are still attached to the notion of confirmation, the scientific community has solved this problem by declaring defeat on a strict, formal notion of evidence. You will never open a scientific paper to find a number that purports to be the degree of confirmation of a theory. Watson and Crick never said "our degree of confirmation in DNA being a double helix is 79.4." (You will however open papers to find precise numbers on statistical theories implied by a general theory. I'm getting to this.)

Instead of formally comparing the evidence in favor of various theories, we compare theories in other ways. We first ask that they satisfy certain criteria—such as not being post-hoc, not being more complicated than necessary, and not invoking essences.¹ And we also demand that they make predictions beforehand that we can go and test. When there are multiple live hypotheses on the table we try to design tests that will distinguish them from each other, ideally refuting all but one. But we don't have a way of formally comparing the evidence for one versus the other. We might use the word evidence (in fact we use this word a lot) in reference to scientific theories, but it's always in a squishy, subjective sense.

This, it's worth noticing, is what makes science fun and interesting! If there was a clear cut way to measure the evidence for our theories, a scientist's job would be mechanical and boring. We would simply generate a bunch of hypotheses and find the one with the most evidence in its favor. Hardly exciting enough to spend five years in graduate school losing your hair and making next to no money.

Scientists having a rough time trying to quantify evidence for the prehensile tail theory.

To recap: you run into big issues when you try to formalize the notion of evidence for a scientific theory. So, naturally, we don't do that. We instead compare theories in other ways—both by designing tests that distinguish between different theories, but also by imposing constraints on the types of theories we consider in the first place.

II. ... did we just invalidate statistics?

But there is one discipline where the formal notion of evidence is alive and well. That discipline is statistics. Leveraging probability theory, statistical theory has developed a huge mathematical toolkit for precisely this purpose. We quantify how surprising data is under particular hypotheses (p-values, e-values), say how likely one theory is relative to another (likelihood ratios, Bayes factors), make claims about the probability of making errors in scientific discovery (type-I error rates, FDR control, FWER control), and generally provide guarantees or estimates related to how well-supported various theories are by data (confidence intervals, posterior probabilities, etc).

Statistics, in other words, is in the business of providing the kinds of formal guarantees that we just argued was doomed in science.

This should make us uneasy. What's going on here—is statistics trying to do the impossible? This seeming paradox often leads to two reactions, both of which are wrong, and both of which confuse the boundaries between science on one hand and math on the other.

The first is to believe that if statistics can do it, then science can do it as well. This leads to a misguided belief in the possibility of quantifying the precise state of our scientific knowledge at any point. (I promised myself I wouldn’t name names here …) The second reaction is the inverse of the first. It holds that if science can't do it, then surely statistics can't do it either. That is, the second reaction is to become skeptical of statistics.

Neither of these reactions is correct. The correct reaction is instead to notice that there is no paradox, because science and statistics are playing different (but closely related) games.

Statistics gets out of Hempel's paradox by fiat. The currency of statistics is mathematical models, simplifications of reality that allow evidence to be precisely quantified by construction. A model declares a priori that it only cares about looking at monkeys, not coffee cups, and also makes assumptions about how many monkeys we've seen so far, how we're sampling monkeys, how many monkeys there are in the world, and what is possible to observe every time we look at a monkey.

These restrictions are what allow us to make precise statements about evidence. They're also what makes correctly applying statistical models tricky: we want to make sure that the model matches reality close enough to be useful. But the model also needs to be simple enough that we can actually do things with it. It needs to be amenable to analysis. Finding useful but manageable models is a fine line, and constitutes the art of doing science.

Statistics is the map, reality is the territory and, all together now, the map is not the territory. But the right map can be useful in the right territory. (I had to include a map and territory analogy, sorry.)

III. The role of statistics in scientific discovery

To more formally delineate the world of science and statistics, it's helpful to notice how they interact. In science, we're after general theories of nature. These theories are objective and time-independent, such as "DNA is a double-helix" and "hydrogen has one proton and one electron".

A theory, let’s call it T, implies things about the world. It has consequences. Logically we can write this as T → O, where O stands for "observation", and T→ O means that if T is true then so too is O. If T is "light travels at a constant speed of 299,792,458 m/s in a vacuum," the O might be "radio waves, X-rays, and visible light should all travel at exactly the same speed (in a vacuum) despite having different frequencies."

(This is different from our monkey and prehensile tail example. There we phrased the theory itself as a conditional statement, whereas now we're discussing the implications of a theory.)

When you make implied observations precise enough, you realize they too usually have the form of conditional implications. That is, O can be written as O1 → O2 (if O1 then O2) and we get the deductive chain T→ (O_1→ O_2). In the speed of light example, O can be rephrased to be the conditional statement: if we measure the speed of radio waves, X-rays, and visible light in a vacuum, then they will all have the same speed. If T is "hydrogen has one proton and electron," then O1 → O2 might be "If we heat hydrogen gas to approximately 3000 Kelvin, then it should emit light that includes a spectral line at exactly 656.3 nanometers."

Okay, why does this matter? Because statistics is in the business of testing O1 → O2, not T→ O. We try to carefully craft our experimental conditions so that O1 is met (we set up an apparatus to send and receive radio waves, X-rays and visible light; we heat hydrogen to 3000K), and then check to see if O2 holds.

But there's lots of error and uncertainty in this process! Our measurements will never be perfect—there will be human error, instrumentation error, and overall imprecision. Have you ever tried measuring the speed of an X-ray? It's not all pancakes and blueberries.

As our theories get more sophisticated, the effects we're looking for are often miniscule. When LIGO was looking for evidence of gravitational waves, it was looking for an effect that would stretch and compress the detector's 4-kilometer arms by less than 1/10,000th the width of a proton. The detectors have to be so sensitive that they'll pick vibrations from distant traffic, farming activities, and humans just walking around. LIGO has to pick out the tiny effect of a gravitational wave from all this background noise.

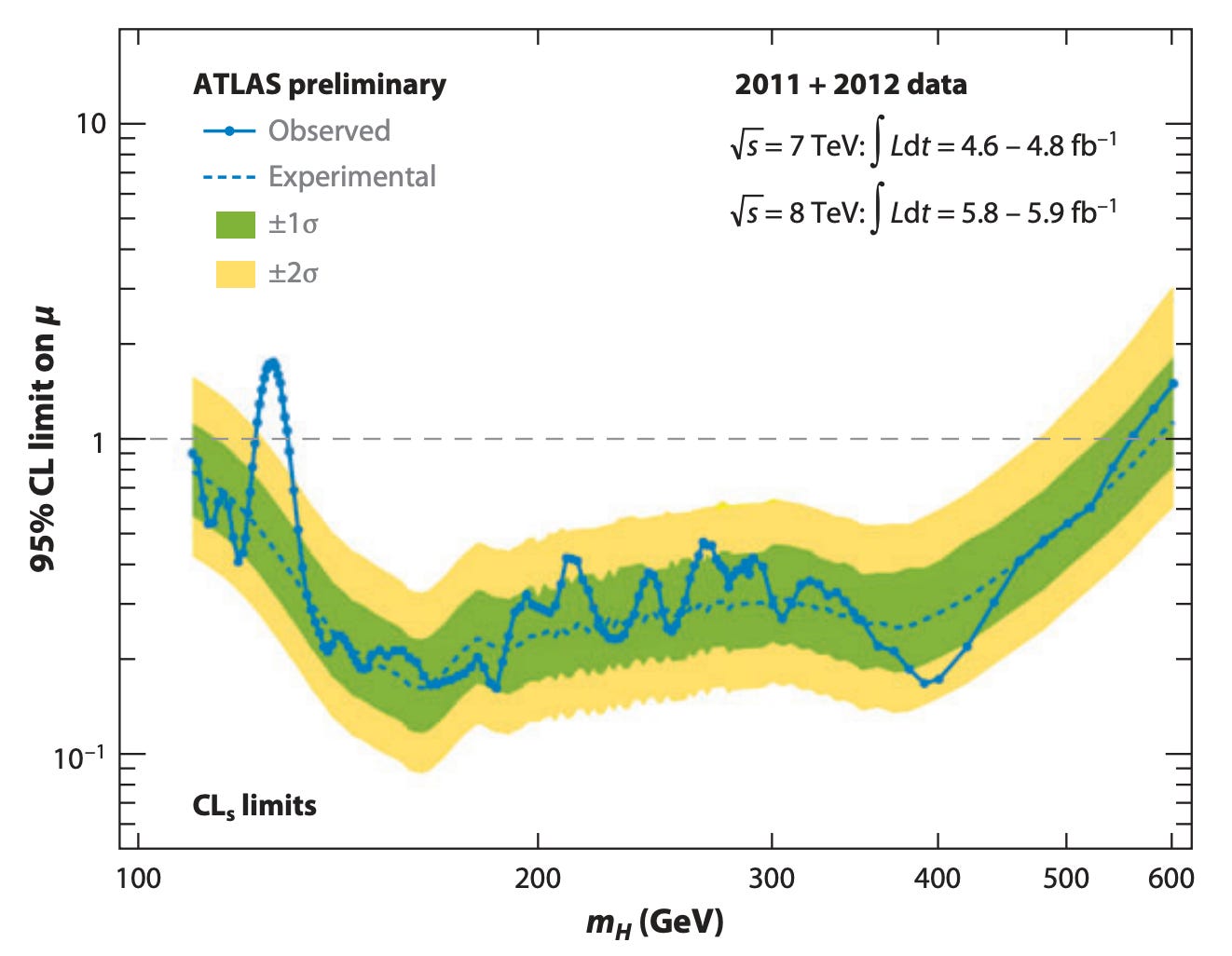
Or take the discovery of the Higgs Boson in 2012 at the LHC. We often say we "found" the Higgs. What does that mean? It means that we saw the blue bump on the left side in the plot below and concluded that it was evidence of the Higgs. We made a bunch of statistical assumptions on what particle collisions would look like without the Higgs (themselves the result of previous theory and experiments) and looked at what "normal behavior" would be under these assumptions. These are the green and yellow bands. Then we saw that the observed data was significantly outside these bounds. Welcome to the party, Higgs.

From The Role of Statistics in the Discovery of a Higgs Boson.

You can argue that we used the wrong statistical model when detecting the Higgs, but it's clear we need statistics. Imagine if all you had was the blue dots in the plot (the "observed" data, not the "experimental" data which, confusingly, is itself part of the statistical model). Would you know that the bump on the left was significant in any way? What about the bump on the right, or the bumps in the middle? Maybe we discovered 17 new particles, actually!

The give and take between science and statistics involves generating implications O1 → O2 which are amenable to statistical models. The conclusions will, of course, always be uncertain—both because statistical conclusions themselves are never certain, but also because we're making simplifying assumptions about reality in order to do statistics in the first place.

So when we discover, or fail to discover something, it's really a statement about the statistical model. And then we hesitantly apply these conclusions to reality if we think our model is good enough. Or maybe we discovering that our simplified model of the world behaves differently than we expected, which then sends us back to refine our theories. Science progresses not by accumulating confirmatory evidence, but through this iterative dance between theoretical insight and statistical testing, none of which is ever on logically pure and rock-solid ground.

1. We used to allow for essences in our theories. Think elan vital and phlogiston. But this got excised from modern scientists because of good critiques from (admittedly over-eager) empiricists like George Berkeley and Ernst Mach.